詳細度数とシェル傾性

これはII章の段階で既に述べたことですが、ある音の伸ばしやすさは、カーネルとシェルの両面から影響を受けます。そして状況によっては、カーネル面の解決とシェル面の解決が「競合」することもある。

これまで「傾性」といえば基本的にカーネルのもつ傾性を指しましたが、今後はここをしっかり区別するために、それぞれカーネル傾性_{Kernel Tendency}、シェル傾性_{Shell Tendency}と呼び分けることにします。

カーネル傾性についてはもうお馴染みですが、その一方でシェル傾性についてはさほど言及してきませんでした。「傾性音でも、それがコードトーンであれば伸ばしやすい」くらいの話しかしていませんね。ハーモナイズ論を進めていく前に、ここもまた整理しておく必要があります。

度数の表記について

この記事からは、詳細度数を用いたシェルの説明をたくさんするので、記号を用いたシンプルな表記を採用していきます。

「増」は「+」、「減」は「o」で表されるということを思い出しておいてください。

1. シェル傾性とは

シェルの本質は、「コード」というより「ベース」との位置関係です。それゆえ「シェル傾性」を考えるにあたっては、コードクオリティを抜きにしてベース音との直接的関係性がまず重要で、それがシェル傾性の多寡の第一基準となります。「コード目線」と「ベース目線」では何が違ってくるのか? 具体例を使って説明していこうと思います。

たとえばV_7sus4においてはソ・ド・レ・ファの4音はみな「コードトーン」ですが、その立場は平等ではありません。ソ・レ・ファの3人はノーマルな奇数シェルで、対するドだけが「サスペンドした4度」という特殊な役割を持っています。そしてドがシへ進むことによって聴き手は「解決感」を得ることができる。

このような場合、ドの音は「sus4」というコードクオリティにとっては「核となるコードトーン」ですが、シェル論においてはそれよりも「ベースと緊張関係にある」という点に着目し、このドは、ソというベース音に対して傾性を有すると解釈するのです。

2. シェル傾性の増加

ただもちろん、V_sus4とV⁽¹¹⁾とでは、ドの伸ばしやすさは違いますよね。これについては、「追加でシが加わった段階でソとシが結束し、ドが邪魔者であると明確に認識されることによって傾性がさらに高まる」と捉えます。

こういうことですね。比喩のストーリーに仕立てましたが、実際に周波数比と協和、それに伴う緊張というメカニズムを考えれば、これに相当する音響現象は現実として起こっているわけです。IV章でやった、「パワーコードやsus4にして濁りを回避する」という方法論は、ここでいう③の傾性増加を起こさないための回避策だったといえます。

つまり、まず第一にベースとの度数関係からシェル傾性のデフォルト値が決まる。これは二者の直接的ハーモニーに基づく出来事なのでコードクオリティは関係ないし、さらにはルートの音度が何であるかも関係ありません。
そしてコードを肉付けしていく中で第二の傾性変化のタイミングが訪れ、そこで傾性が増加も減少もしうる。この2段階構造で考えます。カーネル傾性も含めると合計で3段階ですね。

ごく厳密には②の傾性と③の傾性は分けて論じるべきものなので、必要あらば「ベース傾性」「和声的傾性」と呼び分けることにしますが、基本的には「シェル傾性」という言葉にまとめてしまいます。

この3段階に区分してハーモナイズ作業を考えることで、「ベースとの傾性が強いが、ここはこのメロとベースでしっかり伸ばしたいので、肉付けの段階でうまく傾性を軽減させよう」といった風に、どこで何をすればいいのかが明確になります。

3. シェル傾性の軽減

先ほどは3rdの登場によって4thが追いやられるという「傾性増加」パターンでしたが、逆に「傾性軽減」もできる。それは主だっては、スラッシュコード化によって達成されます。

こうしてみると「転回形」というのは本当に興味深い認知現象で、下克上というか、ウワモノたちの固い結束によってベース音がコードルートの座から失脚してしまうわけですね。

この「スラッシュコード化」によってドのパリティは奇数となって伸ばしやすくなりますが、しかしベースとの傾性が消失したわけではありません。これは二者の直接的関係であり、後から変わることはない。だからこそI_/Vは普通のIよりずいぶん安定感には欠けるし、それゆえ同ルートであるVへの解決が望まれるのです。

スラッシュコードにおいては、コード感に対する度数とベースとの直接的度数、この両方を考慮しなくてはいけないということですね¹。

そしてVにおいてはドよりもシの方が低傾性で収まるということから、カーネル傾性を上書きするだけの力がシェル傾性にはあると言えそうです。いわばこれはカーネル傾性とシェル傾性の掛け算みたいなもので、奇数シェルはシェル傾性がゼロ。だからカーネル傾性がなんであろうと、ゼロをかければゼロになる。そんなイメージですね。

上方避難・下方避難

また、普通にやったら傾性が増加してしまうようなコード付けであっても、ヴォイシング(配置)の工夫次第でそれを回避することもできます。例えばさっきのVにおける「ドとシのケンカ」については、シをドよりも上に配置するだけで状況がずいぶん変わります。

これにより、「短2度」関係だったのが「長7度」に転換するため、聴覚上の印象として、嫌な濁り方ではなくなります。

こちらはその実践例。Bメロ2小節目「会って」のところで、メロディがド、ストリングスが高い位置でシという配置になっています。これにより、「和声的傾性」の増加を“ある程度緩和”していると言えますね。このテクニックは発展的なハーモナイズにおいてカギになってくるので、これを避難_Escapeと命名しておきます。

避難 _(Escape)

2つの音が半音差でぶつかっている場合に、片方を適切にオクターブ上下させることで濁りを緩和させること。

半音差の2音のうち、下の音をオクターブ上へ動かすのを「上方避難」、上の音をオクターブ下へ動かすのを「下方避難」と呼ぶ。

上の音をオクターブ上へ、あるいは下の音をオクターブ下へ動かしても「短2度」が「短9度」になるだけで濁りのキツさがほとんど変わらないため、これは「避難」とはならない。

4. 異名同音とシェル傾性

もうひとつ具体例を使って、シェル傾性にもっと親しんでいきましょうか。

例えばVIIøにおけるシとファの関係は、トライトーンですので、極めて傾性が高いかのように思われます。しかしこのファの音は、1・3・5度と順当に音を積み重ねることで生まれた奇数シェルの音でもあります。仮にこれをミに解決させると…

カーネルとしては解決、でもこのミはシに対してサスペンドしていて、レへ降りた方が明らかに安定します。そうすると、ミこそVIIにとって傾性を帯びたシェルであることに気づかされます。

確かにこのシ-ファのトライトーンは、強烈な濁りではあります。しかし、Vsus4がVに解決するように「次のルートに進む前に解決しておかないと収まりが悪い感じがする」ような性質はなく、このシというベースのうえでファはしっかりと伸ばすことができる点が決定的に異なります。シェルの理論においてo5の傾性はP5とさほど変わらない、「微弱傾性」だと考えられます。

減5度の傾性について

「強烈な濁りのトライトーンなのに傾性がない」というのはすごく直感に反しますが、それはコード進行の理論がジャマをしています。確かにVIIøは“コード進行中の役割としては”やや不安定なポジションです。でもそうじゃなく、VIIøというコード内部でのメロディの動きを観察するのがシェルの理論ですから、こういう食い違いも起こります。

例えばsus4のようにメロがP4を位置取って吊っているときは緊張がもたらされますが、「完全4度」という音程自体はよく協和する音程ですよね。こういった点を見ても、このシェル傾性という概念は単に周波数の協和度だけで判断されるものではないのです²。

それゆえ、トライトーンといっても異名同音である増4度の場合はまたシェル傾性が異なります。

減5と増4で傾性が違う？

こちら、ひっくり返してファがベース、シがメロという状態。この時のシは「ファ-ソ-ラ-シ」数えてと四番目の音、増4度になります。ご覧のとおり、たったの半音上がれば極めて安定した完全5度関係が作れるわけなので、ここは解決の欲求が生じています。

こうやってカーネルの異なる増4度たちを集めてみると、納得できるかと思います。「半音上行して完全5度へ達した方が安定を得られる」という観点から、増4度は比較的強い傾性を持ったシェルであると言えます。

• 減5度
  隣接する音度が4度・6度という偶数パリティの音になるため、隣接音へ進んでも解決感は得られず、解決の欲求は生まれない。したがって、「傾性が無い」とみなされる。
• 増4度
  隣接する音度が3度・5度という奇数パリティの音になるため、隣接音へ進んだ方が音響が安定する。したがって、「傾性がある」とみなされる。

ですので、たとえ増減音程だったとしても、パリティが奇数か偶数かというのがひとつの大きな傾性測定基準になるのです。

5. シェル傾性のまとめ

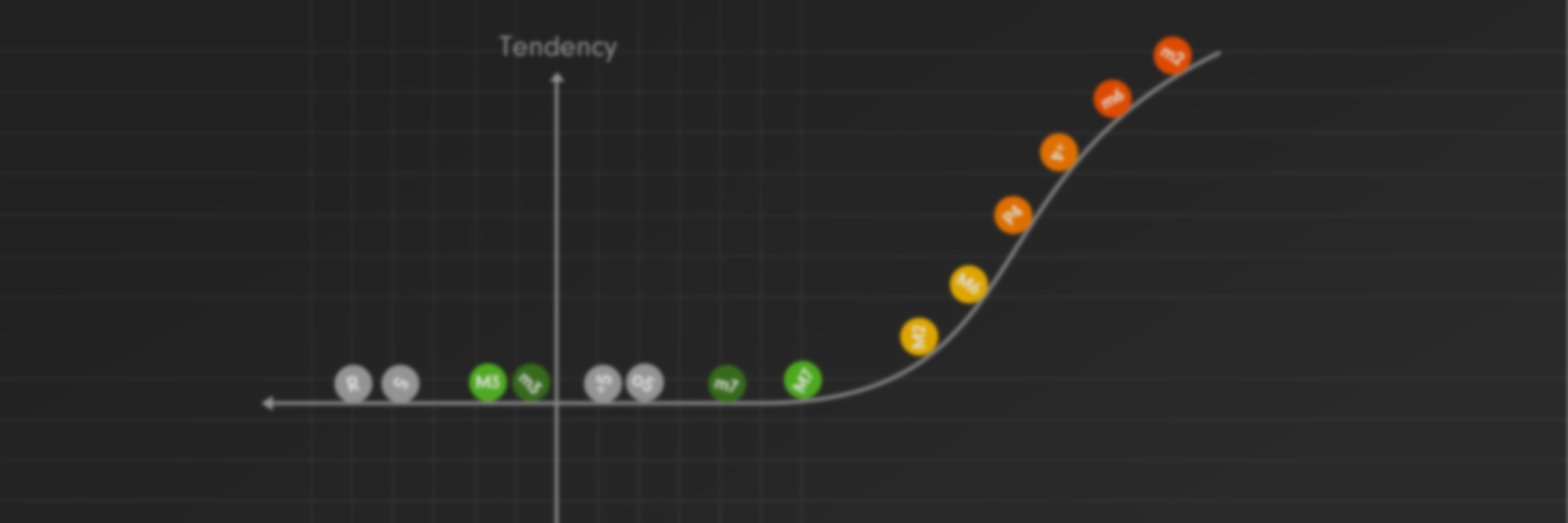
だいたい話が見えてきたところで、主な度数たちのシェル傾性を比べて一列に並べてみます。

奇数シェルは全員「無傾性」でまとめていいレベルですが、強いていうなら7度は「ルートに進むと安定する」という点で非常に微弱な傾性を持っているとも言えそうです。

偶数の方は、「カーネル傾性」の影響もあるし比較は困難です。今回は従来のテンション/アヴォイド論との実践上の互換を優先してこんな序列にしましたが、ここはハッキリ言って個人の感覚差も出てくるところかと思います。傾性の具体的な数値化というのは完全に脳科学の域ですので、気軽に提言出来ないことです。傾性論の完全な構築にはまだ科学の進歩を待つ必要があるので、それまではまだ、ある程度あいまいさを残しておくほかない。悔しいですがそういう状況です😭

この傾性の前段階に「カーネル傾性」があって、後段階にベース以外の音との関係から生まれる「和声的傾性」があり、その掛け合わせで最終的な傾性が定まるという図式です。

シェル傾性の強弱は、当然ながらハーモナイズの際の重要な基準になってきます。確実に無傾性で抑えたいという場面もあるし、M2までなら許せるという時もあれば、逆にあえてm6やm2のような強傾性シェルで揺さぶりをかけたいという時もあるでしょう。シェル傾性をしっかり把握するだけでも、ずいぶんハーモナイズ作業が楽になります。

そんなわけでここから先は、詳細度数とにらめっこしながらのハーモナイズ作業へと進んでいきます。詳細度数にまだ不慣れで話がスッと飲み込めない場合には、もう一度IV章を復習したり、あるいはいったん実践での修行に切り替えるとよいでしょう。

まとめ

• ベース音とメロディという二者の度数関係から傾性が発生しえます。この傾性を、「ベース傾性」と呼びます。
• さらにベース以外の音を付け加えた際に新たに傾性が増加することがあり、これを「和声的傾性」と呼びます。
• スラッシュコードの場合には「コードルート」と「ベース」が異なるために、シェル関係は複雑化します。「ベース傾性」と「和声的傾性」を複合して得られる最終的な傾性のことを、「シェル傾性」と呼びます。
• シェルのパリティが奇数であることが傾性に与える影響は大きく、たとえカーネル傾性が高い音であっても、それを打ち消すことができます。
• 偶数パリティにおける傾性シェルについては、M2が比較的微弱、m2が強力といった序列がありますが、カーネル傾性の影響も受けて様々に変動します。

Continue