ネオ・リーマン理論❷ 共通音のネットワーク

3. 音楽理論の数学化

最後に取りあげるネオ・リーマン理論のトピックとして、これはもう実践とは関わりの薄い内容になるのですが、音楽理論をより数学的に記述するというテーマがあります。

これは「ネオ」より昔のリーマン本人が目指していたところで、特に1916年の『音想像論』では、和音の変形を計算で表す試みが見られます。

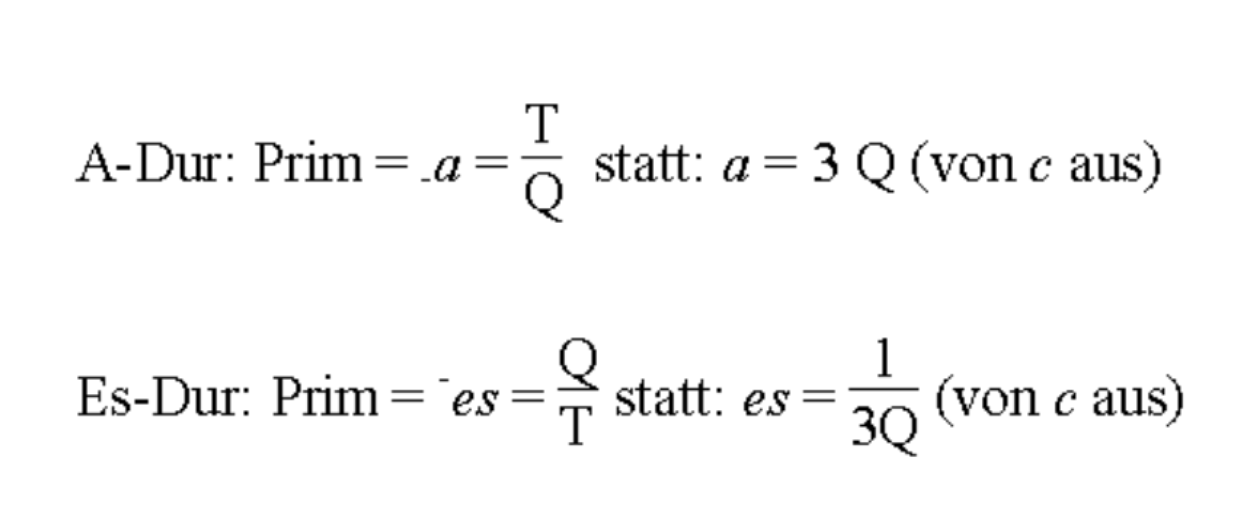Riemann, Hugo. Ideen zu einer ‘Lehre von den Tonvorstellungen’.

こちらQはQuintで「5度」を、TはTerzで「3度」を表し、かけ算(分子)なら上行、わり算(分母)なら下行を表すというもの。
Cメジャーから見たAメジャーは3Qつまり「5度上行を3回繰り返したもの」という五度圏的な見方をする代わりに(statt)、T/Qつまり「3度上行と5度下行を合算したもの」というトネッツ的な見方をしよう……というような主張を展開している場面です。
前回もD操作の逆をD⁻¹とするなんて話がありましたが、そうした数式的な所作はリーマン本人の遺志を継いだものだったわけです。

ただ確かに上の式を見るとa=T/Qというふうにイコールで結ばれていて、左辺はコード、右辺はコードの進行というちょっと不自然な等式になっています。Q,Tが和音の変形操作を指すのか、はたまた和音そのものへのラベリングなのか微妙な具合です。Q3つぶんをQ³でなく3Qと書いているところにも、Qを単に「5度」という数量として見ていたような雰囲気があり、ここにはとにかく過渡期の感じ、何かを掴みかけてはいるが完成していない感じがよく表れています。

おそらくこういう部分を指して論者たちは「自分が変形理論を着想しているという自覚が足りなかった」と評しているのでしょう。リーマンはこの著作の3年後に70歳で亡くなってしまっているので、あと10年長生きしていればリーマン自身が変形理論を打ち立てていたのではという気配すらして、なおさらそれが惜しく思われます。だからその遺志を継いでこのアイデアを一歩先のレベルへ進めようというのもネオ・リーマン理論のトピックのひとつなのです。そのためこの記事でも少しだけ、こうした数学寄りの部分を紹介しようと思います。

ピッチクラス

まずこれはネオ・リーマン理論に限らずもっと広く使われている仕組みですが、音名をABCで表す代わりに0~11の数字で表すやり方があり、これをピッチクラス_{Pitch Class, pc}といいます。

ピッチクラスはABC音名の代替的存在であり、オクターブの上下は関係ありません。つまり、例えばpc=7のオクターブ上の音をpc=19としたりはせず、12を超えた分は余りをとって同じくpc=7とします。
数字にすることでより数的に音関係を見ることができるほか、異名同音を無視する点に大きな意義があり、調性というコンテクストがない状態で論じることの多いネオ・リーマン理論にとってピッチクラスはすごく便利な存在です。

例えばトネッツも、しばしばABC音名の代わりにこのピッチクラスを用いて描かれます。

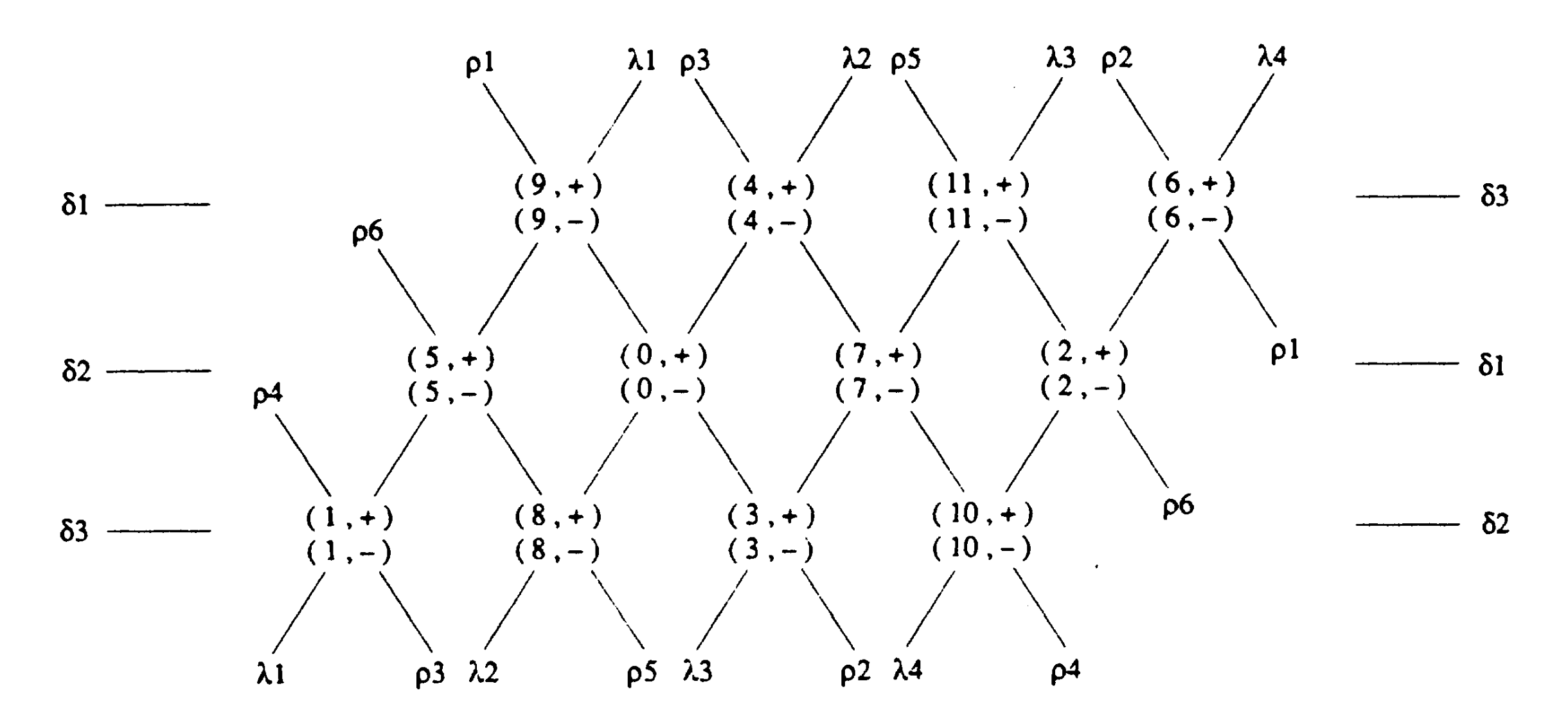Hyer, Brian. Reimag(in)ing Riemann.

数字の横に書かれた±は前回の記事でもあったメジャーコード/マイナーコードを表すネオ・リーマン理論内の記号で、したがって(0,+)はCのメジャーコードを意味するといった具合です。音を数字で表すことの意義は大きく、様々な計算操作が記述しやすくなるほか、例えばD操作のDを音名のDと取り違えるみたいなややこしさも避けられますよね。

ピッチクラス・セット

音階のように音名をいくつか集めたものをピッチクラスで表現することももちろんあり、その集合はピッチクラス・セット_{Pitch Class Set}といいます。Setは数学の「集合」を意味する単語で、これはつまり「部分集合」とか「基数」とか、集合論で使われている用語を丸ごと音楽理論へ転用しようという企てでもあります。

例えば「パワー・タワーズ」の各塔に使用するドミナント・ディミニッシュ・スケールのメンバーが、次のように数字の集合で表されていたりします。

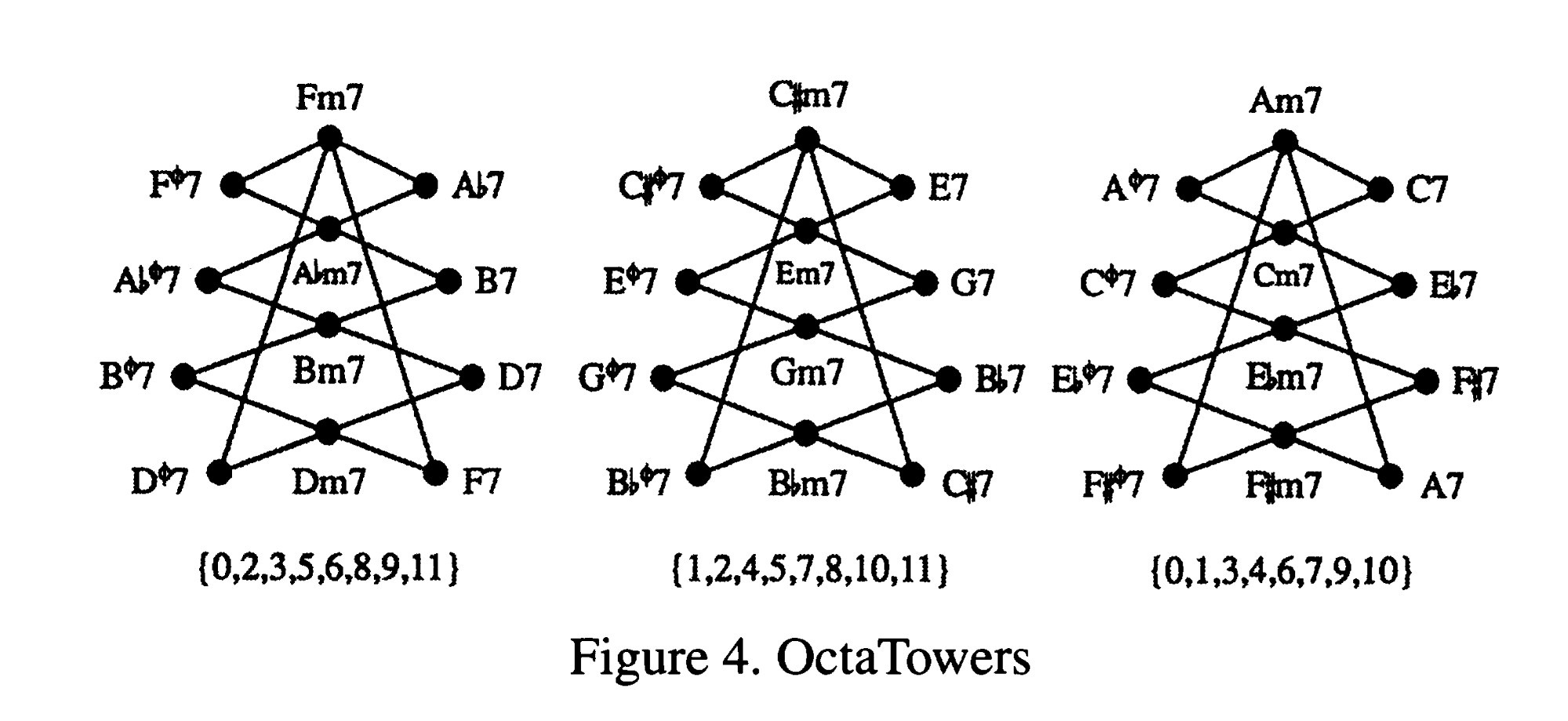Douthett,Jack. Steinbach, Peter. Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.

ピッチクラス・セットはこのように{}や[]で括ってそのまとまりを表します。{0,1,3,4,6,7,9,10}という数字で並ぶと、半全半全…というドミナント・ディミニッシュ・スケールの間隔がクッキリと見えますね。またオクタトニック・スケールにつきものの異名同音のスペリング問題も全く気にせずに済みます。

ピッチクラス・セットを用いて数学的に発展させた理論はそのままピッチクラス・セット理論_{Musical Set Theory}と呼ばれ、これはまたネオ・リーマン理論とは別系統の理論として発展しています。

一般化された音程システム(GIS)

それからネオ・リーマン理論の先駆者であるデビッド・ルーウィンは1987年の著書で一般化された音程システム_{Generalized Interval Systems, GIS}と銘打って、音程の記述法をもっと数学的でマトモなものにアップデートすることを提言しています。その一番基礎的なところを引用すると……

Given pitches s and t, int(s, t) is the number of scale steps one must move in an upwards-oriented sense to get from s to t. Thus int(C4, C4) = 0, int(C4,D4) = 1, int(C4,E4) = 2, and int(C4,C5) = 7. Int(C4, A3) = –2, since moving “–2 steps up” amounts to moving 2 steps down. …… This obviates a defect in the traditional measurements which tell us, for example, that a “3rd” and another “3rd” compose to form a “5th.” (3 + 3 = 5 ???)

与えられたピッチs,tに対し、int(s,t)はsからtに至るまでに上行するスケールのステップ数を指すものとする。したがってint(C4, C4) = 0, int(C4,D4) = 1, int(C4,E4) = 2, int(C4,C5) = 7 となる。そしてInt(C4, A3) = –2 である。というのも、「-2ステップの上行」が2ステップの下行を意味するからだ。(中略) これにより、例えば「3度にさらに3度を重ねると5度になります」などという慣習的測定法の欠陥を取り除くことができる。(3 + 3 = 5 ???)

Lewin, David. Generalized Musical Intervals and Transformations (p.16).

ここでは「⚪︎度下」という言い方の代わりに負の数を用いること、そして何より我々をずっと苦しめている「ゼロ距離=1度」問題を解決しようと挑んでいます。仮にこのシステムが普及すれば、「3度下のハモリ」は「-2度ハモリ」となるのでしょうか。既存のシステムを完全に置き換えるまでこれを浸透させるのはかなり困難な道のりですが、現在の「移動ド」のように一定の勢力となる可能性なら十分ありそうですね。

なんにせよ浸透しようがしまいがこうしてキチッと標準化を目指す書式があるというのは有難いことで、どうしても0-indexedの度数表記で何かを書きたいというとき、「ルーウィンのGISを採用します」と一言添えればそれで済むわけです。誰もが諦めていたこの不都合に「もう1回ウチらの世代からやり直そうや!」と旗揚げしたことも、ルーウィンの理論が注目された理由の一つかもしれません。

PLR操作の一般化

ネオ・リーマン理論は現在クロマティックな音楽の分析に活用されていますが、基本であるPLR操作はその生まれがゴリゴリにダイアトニックであり、それゆえI-viに由来する短3度下行(R)とI-iiiに由来する長3度上行(L)にだけ名前があるという、まずそもそもこの状態が数学的に美しくないですよね。リーマンの遺志を継ぐという建前ゆえかココを弄ろうとする論者はあまりいなかったようですが、音楽学者デビッド・コップは2002年の著書にてこの“聖域”にメスを入れています。

彼はルートの移動量と、メジャー/マイナーのクオリティ転換の有無をもとに、変形操作にシステマティックな名付けをすることを提唱します。

すべて「下行」の操作が第一で、「上行」はみなマイナス1乗で表現するというルールになっています。MはMediantの頭文字ですね。FはFifthが由来で、先述の『音想像論』が英訳された際QuintがFifthに翻訳されたという経緯があります。コップはここにP操作とS操作を加えて、これらを基本操作の全てとしています。

Kopp, David. Chromatic Transformations in Nineteenth-Century Music

ここではPLR操作にあった「メジャーかマイナーかで操作が異なり、同じ操作を2回すると元に戻る」という二元論的世界観は破棄されていて、とにかく機械的であることを優先しています。コップはこの理論を、ダイアトニック的で二元論的であった従来のシステムに対置する意味を込めて半音階的変形システム_{Chromatic Transformation System}と名付けました¹。

ダイアトニック的音楽観を引きずっていたという意味では“負の遺産”であったPLRに決別を告げたのは意義のあることですが、しかし個人的には長短転換の有無でアルファベットを変えてしまうというのはあまりスマートな策には思えません。それこそプラスマイナスでメジャー/マイナーを表す慣習があるのだから、長短の転換はマイナスをかける動作にすれば良かったのでは……などと疑問を覚えるところです。とはいえこれも20年前の本ですから、現在はもっと議論が深められているかもしれません。

音楽の幾何学

せっかくトネッツやキューブのような幾何学的な図形で音を表現するのだから、より幾何学的に音楽を論じようというムーブメントも熱が高まっており、その中で注目を集める著作のひとつがドミートリィ・ティモスコー(Dmitri Tymoczko)の”A Geometory of Music”, 『ある音楽幾何学』です。

この本はルーウィンのGISのように「あるピッチpをχ半音上げる動作をT_χ(p)と呼ぼう」といった基本操作の関数化から始まり、トネッツで単音や和音の動きを図画化したもう一歩先のアイデアとして2つの声部の音程変化(声部連結)の図画化を試みます。

Tymoczko, Dmitri. A Geometry of Music(p.74).

これは、2音のピッチの組み合わせを斜めに配置して座標系にし、声部連結の動きを線で表せるようにしたもの。音程をあえて斜めの格子状に配置しているのは、これにより完全な(度数の全く等しい)平行移動は真横の線、完全な反行は真縦の線になるというメリットを買ってのことです。この空間は、2音のコード・スペース_{Chord Space}と名付けられています。声部連結が「長さ」と「方向」という2つのパラメータを有する矢印によって表されることで、声部連結の数値化やさらなる計算的理論へ発展していけそうです。

そして2和音の座標が2次元空間で表されるので、必然的に3和音の関係は3次元、4和音も4次元なら表現できるという話になり、4次元を表現した図画であるハイパーキューブ(超立方体)の頂点にパワー・タワーズの要領でコードを置いた図が示されます。

Tymoczko, Dmitri. A Geometry of Music(p.106).

3次元的な見方でこのキューブを捉えようとすると当然ながら空間がねじれていてエッシャーの騙し絵を見ているようになってしまうのですが、純粋に頂点と各辺に注目すると、キューブ・ダンスと同様にして「同じ向きの辺は同じ音変化を表す」という特徴がしっかりと表現されていることが分かります。
他にもこの本では「調性」の定義を改めて問い直し5つの要素を提示したり、コード構成音のオクターブ移動や並べ替えといった基本操作を5つピックアップしてそのイニシャルから“OPTIC”と名付けたりなど、かなり基礎からもう一度しっかり定義しなおすぞという気概のうかがえる一冊になっています。

これよりもさらに数学寄りになると「集合論」や「トポロジー」といった数学の専門的な分野にどんどん足を突っ込むことになり、いよいよネオ・リーマン理論とは呼ばれない別領域になりますね。

Alvarez, Alberto. Longoria, Pablo. A Framework for Topological Music Analysis (TMA)

ネオ・リーマン理論も含め、こうした数学的な音楽理論を総称して数理音楽理論_{Mathematical Music Theory}と呼んだりします。

4. 総括

さて、2記事に渡って紹介を続けてきましたが、ひとくちに「ネオ・リーマン理論」と言ってもその内容や趣旨はかなり広範に及ぶことが見えてきたかと思います。改めてその中核的なトピックをまとめると以下のとおりです。

• 和音の変形操作を記号化する。
• 根音ではなく共通音に注目し、声部連結の倹約性から和声を論じる。
• 単音や和音の関係を図画で表し、幾何的に和声を論じる。
• 音楽理論の様々な要素を数式化し、代数的に音楽を論じる。

そして論者どうしが互いの文献を参照しながら議論を繰り返していて、21世紀の今でもまだ発展途上にあります。

リーマン理論からルーウィン理論へ

ところでネオ・リーマン理論の内容は結果的にリーマン本来の理論とはずいぶんかけ離れたものになっているため、「ネオ・リーマン」という言葉はリーマンの名をappropriate(利用,私物化,領有)しているという批判がしばしばなされます²。

例えば根本的なところで、リーマンの「導音転換」は確かにCからEmを導くものですが、これによって出来たEmの和音は「見せかけの協和和音」であって本物のEmと同一ではないというのがその趣旨でした³。そこへ来てネオ・リーマン理論は導音転換を単に「CからEmを作る変形」として使用しているわけですから、確かにいいように名前を借りて利用している感はちょっとあります。

そもそもこうした変形理論が「ネオ・リーマン」と呼ばれるようになったきっかけは、草分けであるルーウィンが1982年の著書にて自身の研究を「リーマン・システム」と名乗ったことにありますが、その命名理由は「リーマンの研究と精神に関連しているから(associated with the spirit and work of Hugo Riemann)」というもので、この時点ではさほど具体的にリーマンの理論を継承してはいません。彼がPARやRELの操作を定義したのは5年後の別の書籍でのことです。こうした点を鑑みて、リーマン研究に詳しい西田紘子氏は次のように述べています。

ここから分かるのは，ルーウィンが，リーマンの著作等を直接に参照・引用したというよりも，和声理論の代表者としてのリーマンの名を象徴的に利用したという点である。(中略) リーマンの名や概念の利用は，ルーウィンにおいて一種の権威づけとして作用し，しかもそれは成功したと言える。
西田紘子. ネオ・リーマン理論のリーマン受容にみる概念変容(p.10).

この「リーマンの名を不当に利用していないか」という観点はけっこうセンシティブなところで、各著者の語り口にはここへの配慮が見え隠れすることがあります。

例えば先述のコップは導音転換の記号Lを大胆にも破棄しましたが、これに際しては「無くすのは惜しまれるのですが」と白々しい前置きをし、「メジャーは大文字、マイナーは小文字にするのがコード界の長き伝統なので…」と慣習を盾に用い、最終的には自分こそがリーマンの後期理論の「意向と精神に忠義を尽くしている」と主張します⁴。ここには先行研究を書き換える罪悪感が感じられると共に、自身がリーマンを不当に利用してはいないという潔白の主張、ひいてはより正統なラインに自分を位置付けたいという密やかな“継承戦”の相も垣間見えます。

ただいずれにせよ理論が発展していく中でいつまでもリーマンの名を冠し続けることへの問題意識からかコップ自身も「半音階的変形システム」という新しい名前をつけたりしていますし、リーマンの系譜にあるかなしかを問わないより広範囲を指す名称として変形理論_{Transformational Theory}という言い方もあります。
あるいは近年ではなんならLewinian Theory、「ルーウィンの理論」とまで呼ばれ始めています⁵。ルーウィンももう亡くなって20年が経ちますが、リーマンという“虎”の威を借りねばならなかった40年前から始まって今や理論が彼の名を冠して広まっていっているところには歴史の積み重ねを感じます。

リーマンは踏み台にされたようでちょっとかわいそうですが、でも彼もハウプトマンやエッティンゲンといった先人たちのアイデアの上に立って自身の名を残したのであり、これは音楽理論史にとっては真っ当な流れというものです。もうさらに40年もしたらもしかしたら「ルーウィン理論」の名が一般的になり、いずれは「ネオ・ルーウィン理論」が唱えられる日が来るかもしれません。

誰が何したかまとめ

今回記事中で登場した話や人物を大まかにまとめると、以下のようになります。

もちろん上に挙げた以外にもたくさんの研究者が関わっていて、特に今回の記事中ではネオ・リーマン理論に対する批評を加えた人物などにはほとんど触れられませんでした。またあくまでも代表的な論者を抽出したものなので、時系列的に彼らより早く上記の内容を唱えた人間がいるかもしれないことは可能性として否定できません。
とはいえルーウィン、ハイアー、コーンの3人が最も主要なキーパーソンという感じで、ネオ・リーマン理論を深掘りしたい場合はまずこの3人の著書から着手するのが良いのではと思います。

これまでジャズ理論に古典派和声、中心軸システムにLCCと紹介してきましたが、いずれも5度関係が理論構築の基盤であり、いつも五度圏がその理論美を象徴していたという意味では全く多様性がなかったとも言えます。

コップは、ルーウィンがドミナントの動きを自然法則だとか音自身が持つ本有的な傾向などではなく音楽に関わった人間の意図的な行為(act)であるとした点が、目的論的なパラダイムへの強い拒絶表明となったと評しています⁶。一方向に回り続けることを宿命づけられたかのような五度圏と、常に複数の道筋が示唆されるトネッツやキューブ・ダンス、パワー・タワーズ。このビジュアルの違いはまさにそういったパラダイムの違いを象徴していると言えます。ネオ・リーマン理論、もとい、“ルーウィンの変形理論”は、5度進行を基礎としない音楽を制作/分析する際の心強い指針となりうるでしょう。