目次
3. トネッツ(Tonnetz)
リーマンは以前紹介した『Harmony, Simplified』の出版以降も自身の理論のアップデートを続け、1916年には『Ideen zu einer ‘Lehre von den Tonvorstellungen’』、日本語では『音想像論』などと訳される本をリリースしました。
そこでは音楽を受け取る聴き手側の心理についての考察がなされるとともに、音関係の図式化と数式化が取り組まれました。そのひとつが、音関係を網目のように繋げて図示するトネッツTonnetzです1。
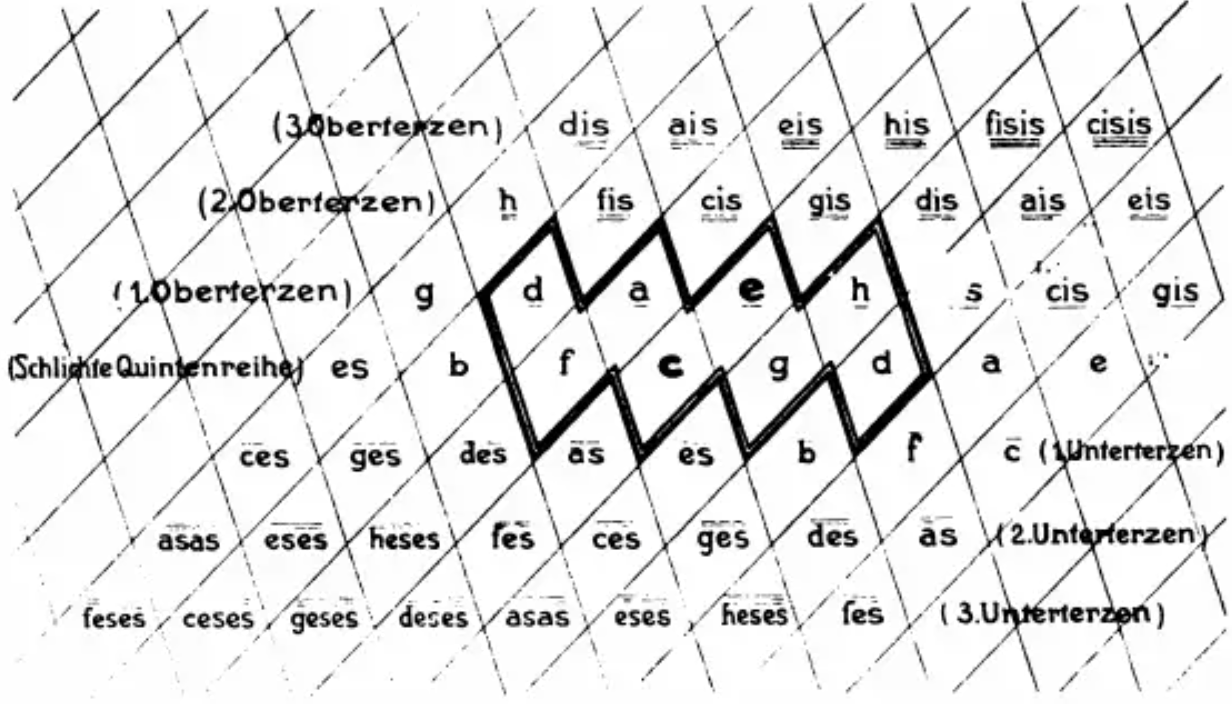 Riemann, Hugo. Ideen zu einer ‘Lehre von den Tonvorstellungen’.
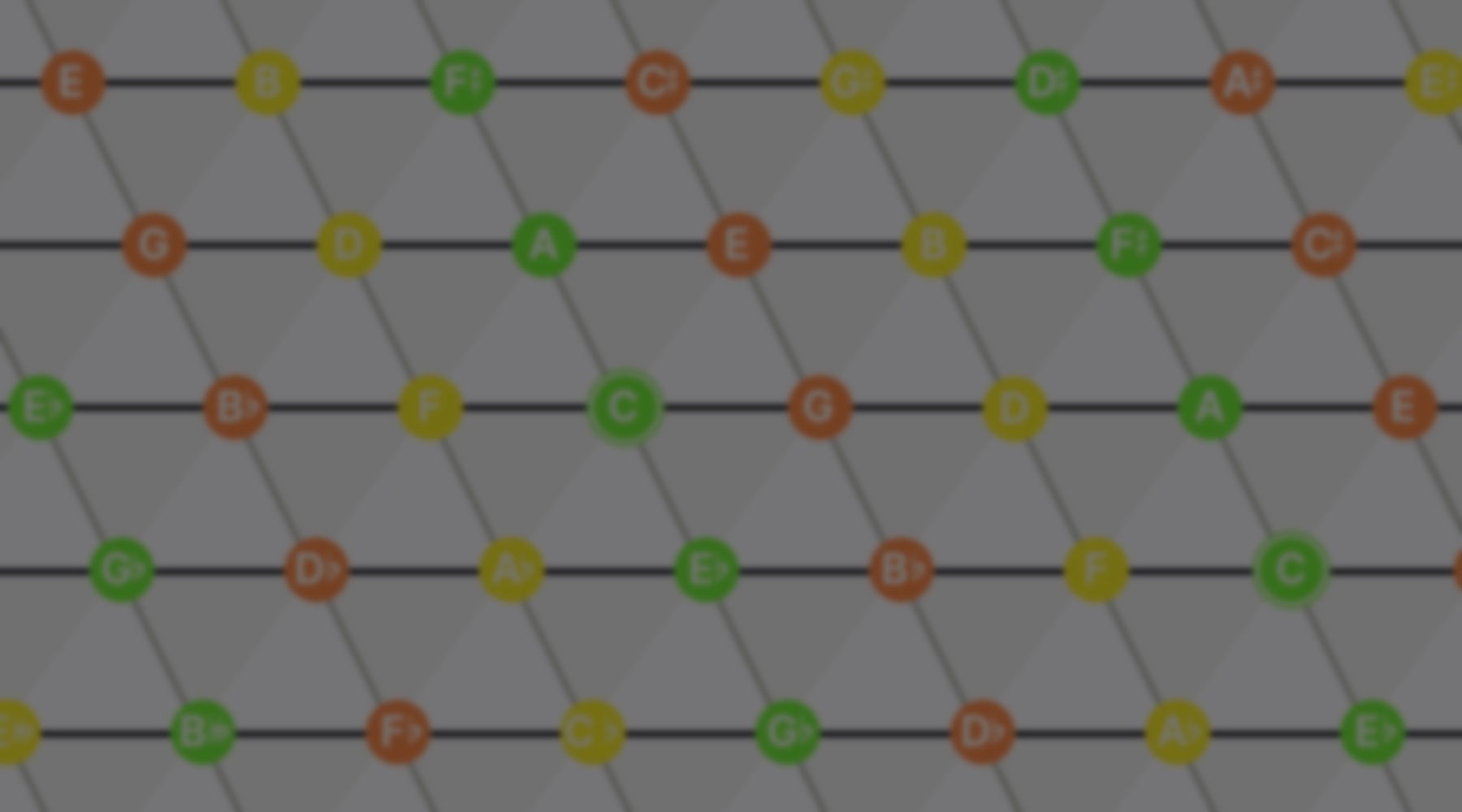
Riemann, Hugo. Ideen zu einer ‘Lehre von den Tonvorstellungen’.Tonnetzは英語で言えばToneのNet、「音の網」という意味です。まずcを中心に見ると左右にはfとgがおり、これは五度圏と同じ完全5度の並びです。その上の段を見ても、g-d-a-eと5度関係で音が並んでいる。さらにcから右上と左下のナナメラインを見ると、e-c-a♭と、これは長3度関係が続くことになります。逆に左上と右下のナナメラインの方はa-c-e♭となっていて、こちらは短3度です。このように、5度と3度の関係による音のネットワークを二次元的に図示したものが、トネッツです。
これまで音関係の図示と言えば「五度圏」でしたが、五度圏は音を単に1本の線で円状に繋いだだけなので、当然ながら5度関係しか明確化されません。対してトネッツは音を縦横の2軸で二次元的に並べることで、5度関係だけでなく長3度・短3度の繋がりまでもを可視化しています。そのため、より使い道が広くありそうだなというのは想像に難くないですね。
現在一般的なトネッツ
トネッツは「横軸を5度間隔、縦軸を3度間隔で表にする」というのがその本質であり、具体的なビジュアライズ法にはバリエーションがあります。斜めにせずカッチリ長方形の格子状にしたものもありますし、上下の向きが逆転しているものもあります。また異名同音をどれくらい区別するかも人によって分かれます。
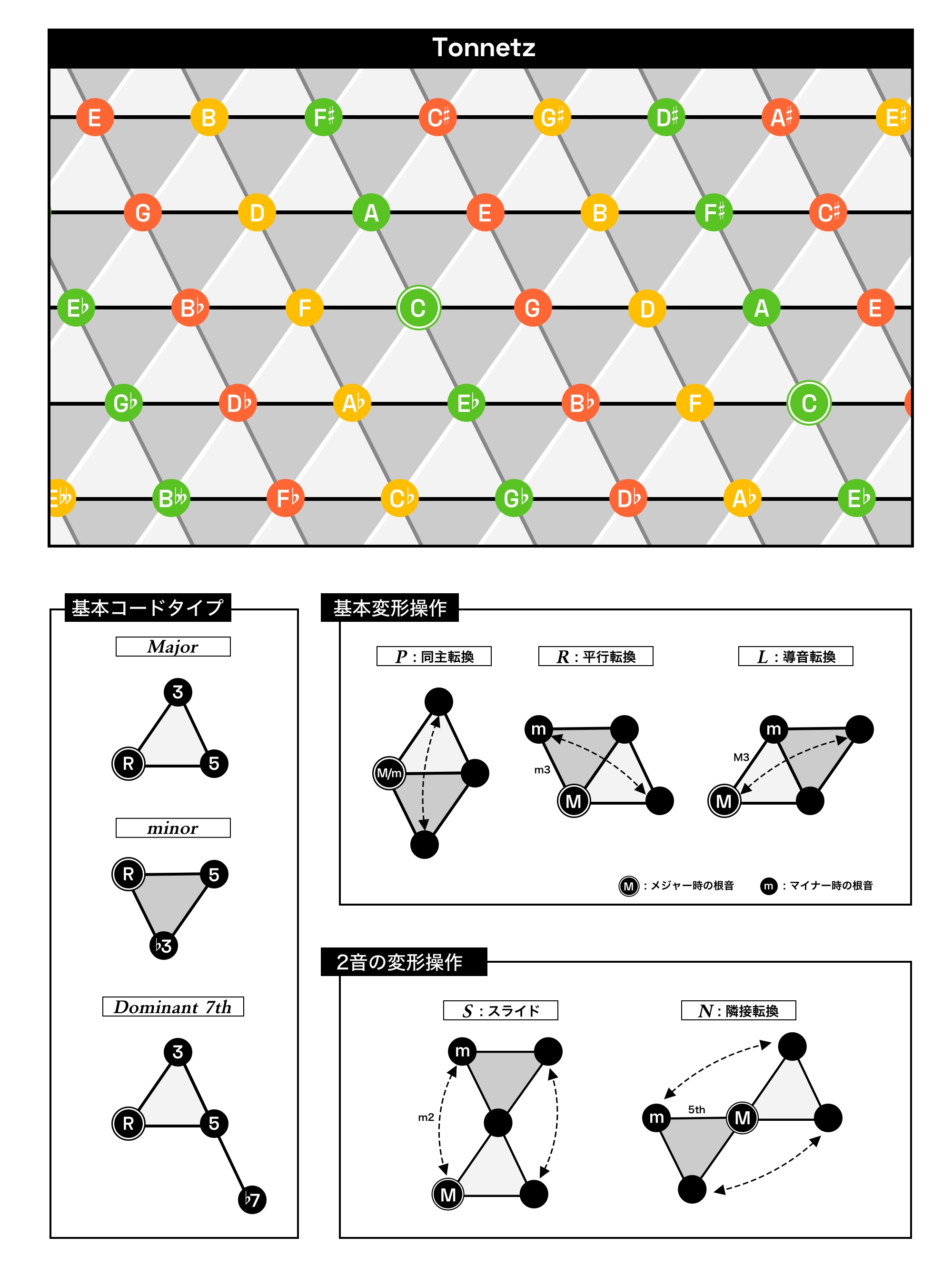
ともあれネオ・リーマン理論で後世の理論家たちが施した改良として概ね広まっているのは、格子の中に音を書くのをやめて、逆に格子の交点に音を置くことで音同士を線で結んだ構図になったスタイルです。
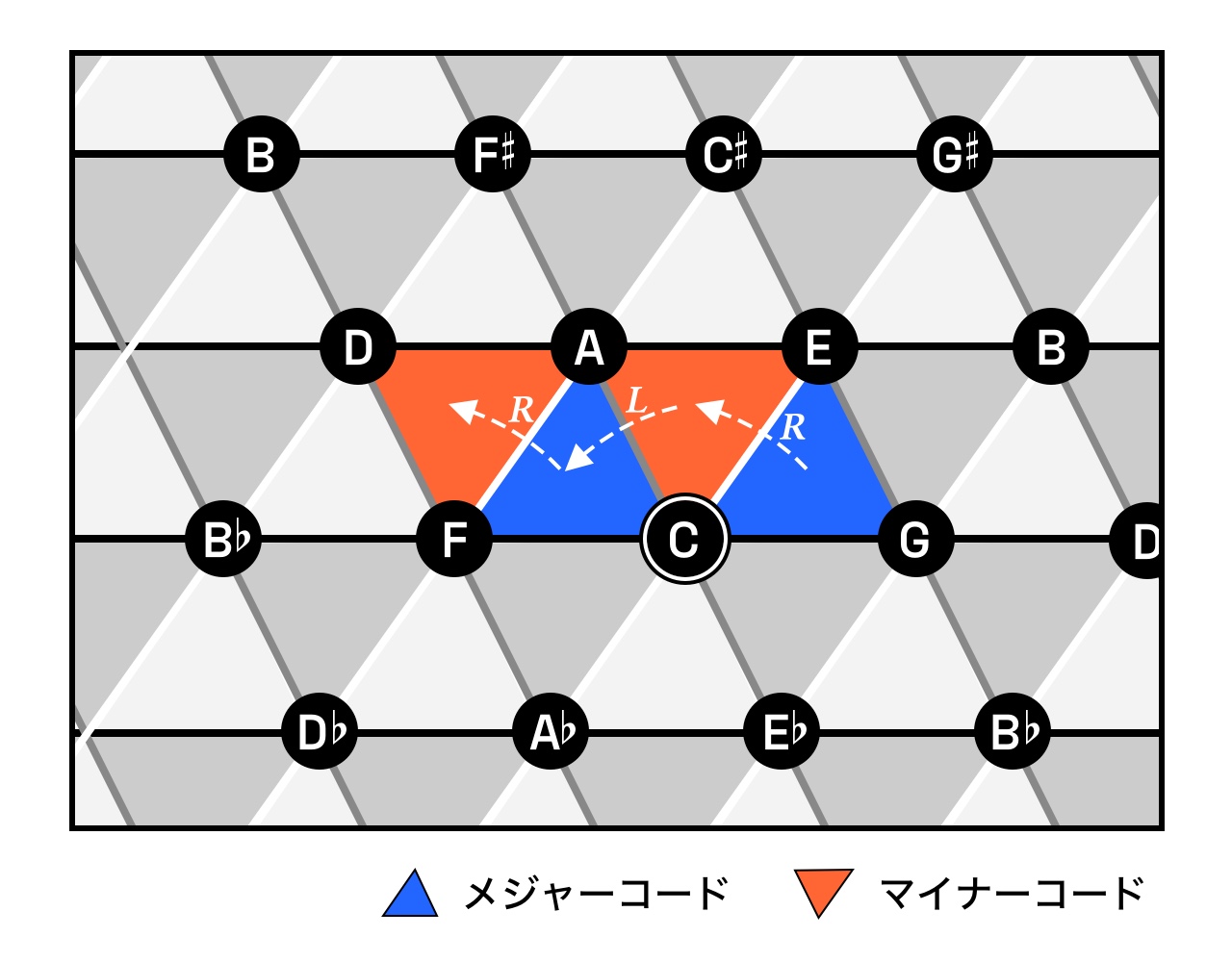
ちょっと情報量が多いので順に説明していきますと、まず音どうしを線で結んだことにより、メジャーコードやマイナーコードのコードトーンを繋ぐと三角形を描くことになります。それゆえ、このトネッツ上に描かれた三角形のマスは、それ自体がコードを表象していることになります。例えばC,E,Gの3点を結んだ直線によって描かれる三角形のマスは、Cメジャーコードのマスということになる。そしてPLRの操作による別のコードへの変形はいずれも、このマスを1マス移動する行為として表現されます。副次的であるS・N操作も、砂時計をひっくり返すような綺麗な対称の動きで表されることになりますね。
トネッツは決してネオ・リーマン理論にしか活用できないものではありませんが、その構造上PLR操作がいずれも隣接マスへの移動となるので、これらを特権化するネオ・リーマン理論とは相性ピッタリの図です。例えば先ほどのベートーヴェンのC-Am-F-Dmというコード進行をトネッツ上で表現すると、以下のようになります。
このように、まるでスゴロクのマスを進むかのように空間的・図形的にコード進行を表現できる。そして、“倹約”な声部連結をする進行ほど三角形が密接した美しい進路を描き出すことになる──。これは明らかに、何か面白いことが色々できそうですよね! 五度圏が調号の増減を示すツールになったり、基調和音を見つけるツールになったりしたように、こういう汎用的な図画は実践においても分析においても有用なアイテムとなり得ます。
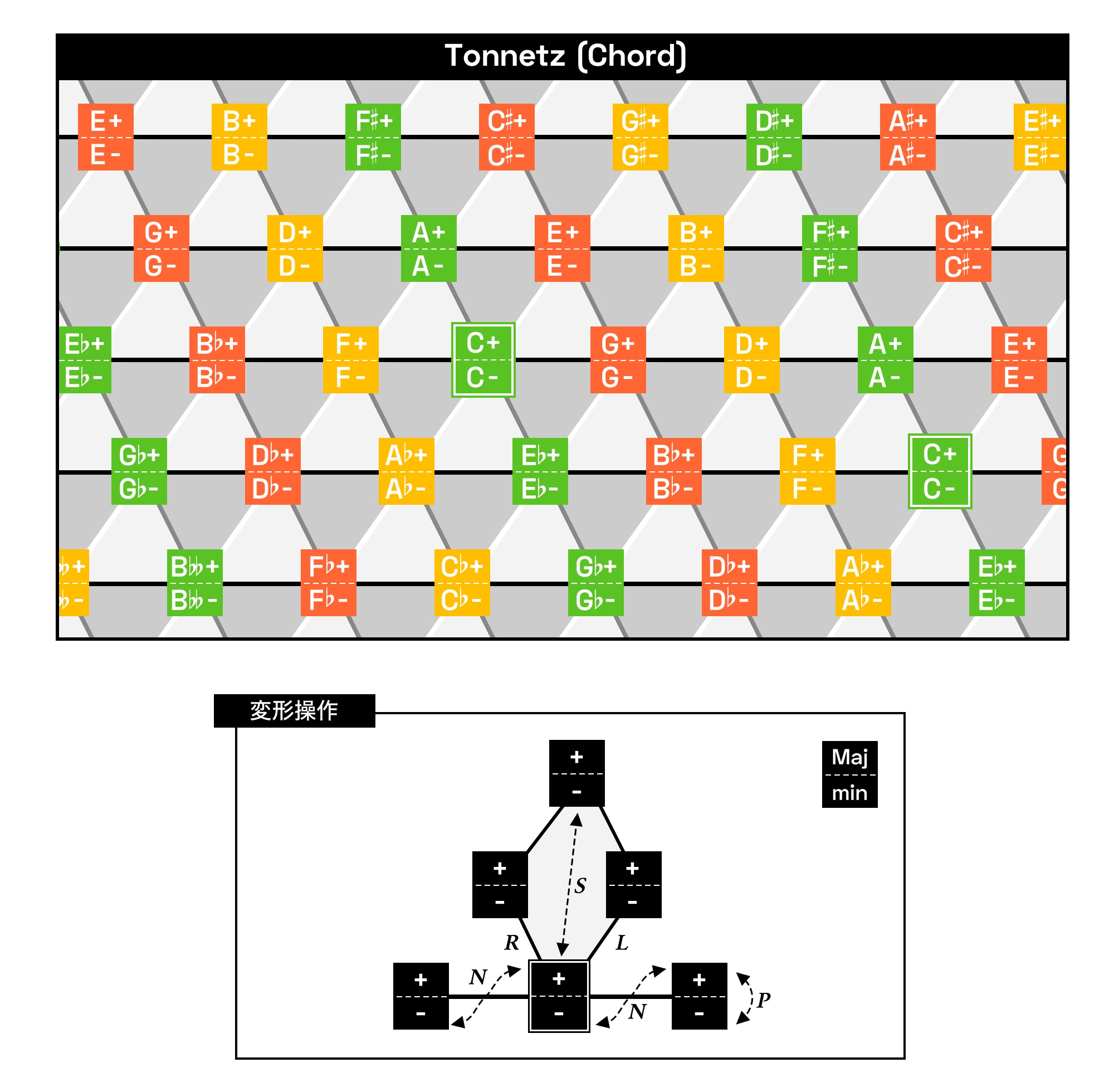
コード版トネッツ
トネッツは単音を点とし和音を面や線で表す図画ですが、そうなると、もし各点がコードを表すような形にすればコードを論じるうえでもっとコンパクトにまとまるのではないかという発想も出てきます。当然これも具体化されていて、次のような図があります。
ネオ・リーマン理論内では、数学になぞらえてメジャーコードをプラス、マイナーコードをマイナスで表記するのが主流であるので、上図ではこれに倣いました(通常コード理論ではプラスと言えばaugなので紛らわしいですが、もはやどうすることもできない)。
この図においてはコード進行は線上の移動によって表されることになって、面で捉えるよりも扱いがシンプルにできそうです。
4. ハイパー・ヘキサトニック・システム
トネッツは音をXYの平面に敷き詰めて無限に広がっていきますが、しかし1オクターブで循環する音楽の世界を映し出すにあたっては、やはり五度圏のように円環構造を描いていた方が直感的な場合があります。例えば先ほどのブラームスのコード進行もA♭-G♯m-E-Em-C-Cm-A♭で1サイクルを成し元の場所へと戻ってきました。これは長3度の連続でオクターブを1周したわけで、もし五度圏ならぬ“三度圏”的な何かがあれば、この循環性をすごく分かりやすくビジュアライズできそうです。
ヘキサトニックの環
それもやっぱり提案されていて、まず以下のような小さな輪を作ります。
これはL・Pの操作を繰り返すと元に戻ってくることを表した図で、長3度離れた3つのルートでの長短和音で計6つのコードがリストアップされます。ブラームスのコード進行は、この環を美しく時計回りに循環する進行であると言えますね。
面白いことに、これらはそれぞれ2音の共通音を持つ非常に“倹約”な声部連結で繋がっているがゆえ、この6つのコードを作るのに必要な構成音もまた全部でたった6つなのです。
このとおり、c,e,g,b,e♭,a♭の6音があればこの6つの和音は作れます。6つの音から6つの和音が作れる。なんだか面白いですね。この円環は、6音から成るのでヘキサトニック・サイクルHexatonic Cycleなどと呼ばれます2。和訳するなら「六音環」などといったところでしょうか。
環を4つ作る
そうなると当然、C,E,A♭以外のルートのペアでも同じ環が作れるぞという話になってきますね。例えば半音上げてC♯,F,Aのルートから環を作った場合は、次のようになります。
先ほどの図をまるまる半音上げただけで、不思議なところは何もありません。ただ興味深いのは、この6コードを作るのに使った6音のうち、c,e,g♯の3音に関しては先ほどの環でも登場していたということです。
まあ先述のSLIDE操作のところでCの3rdであるe音はC♯mの3rdでもあるということを目撃したばかりなので、当然と言えば当然。しかしこの図画には美しさを感じざるを得ないところがあります……!
この調子でDを含む環、E♭を含む環まで作れば、和音の数は6×4=24。つまり12のルートから長短それぞれで合計24個のコードが全て網羅されることになります。それを全部まとめてひとつの図にすると……
こうなります!このように、4つのヘキサトニック・サイクルを配置しその内側に各環の使用ピッチをベン図のような囲いでまとめることで、24コードの関係性をL・P操作を中心としてまとめあげたこの図のことを、ハイパー・ヘキサトニック・システムHyper-Hexatonic System(HSS)といいます3。
この図においてはまずL・P操作が円環内の循環として表現され、ルートの半音移動や5度進行は隣の環への移動、全音移動やトライトーン進行は向かい側の環への移動となります。それから、C↔︎A♭mのように環内で向かい合う反対側に移動する操作は特段の意味があるということで、H(hexatonic pole)と名付けられました。この図においては、R操作のビジュアライズは重視されていません。
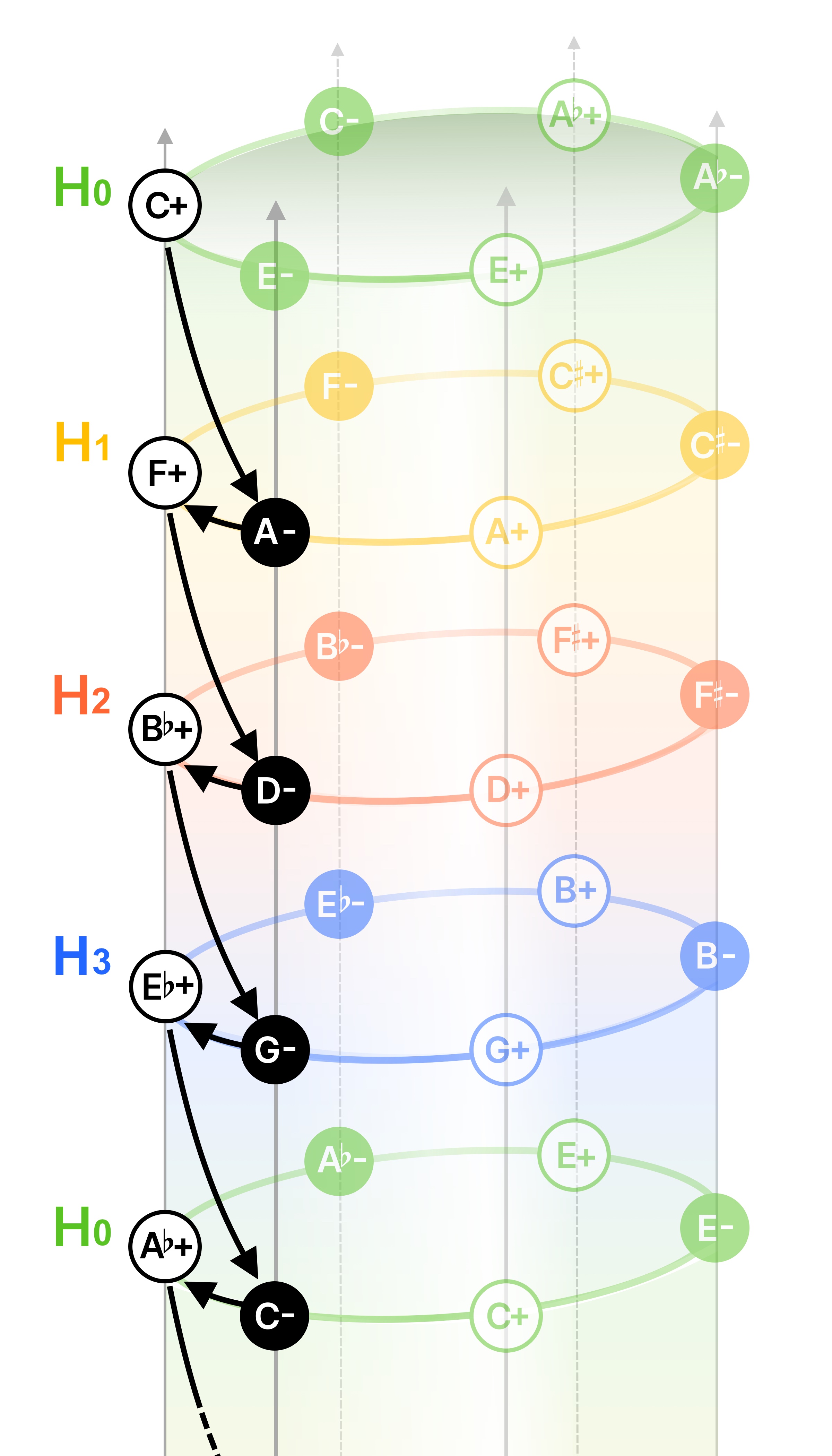
六音環のシリンダー
R操作や5度関係の重要性を鑑みてそれらの接続もある程度分かりやすく図示したいという場合、環を縦に重ねて5度関係を串刺しにするとシリンダー(円筒)状のビジュアルとなり、より多くの操作を簡潔な線で結ぶことができるようになります4。
こちらの方が立体図形として表現しているぶん、関係性の表現力では優ります。5度で繋ぐことを優先した場合上のH0と下のH0では円環の角度が120°回転しているというのも興味深いですね。
このビジュアル上では、例えば先ほどのベートーベンのRLを連鎖させる進行は円筒の側面の一部分を滑り落ちるような動きで表現されることになります。
こうして分析に使うのも楽しいですが、制作の際にこの図をヒントにして新しいコード進行を考えてみるのも面白そうです。
補完的理論としての意義
このように、PLRの変形理論は3度進行に特化しているがゆえ、5度中心の理論では瑣末なものとして扱われてしまいそうな美しい3度の動きや半音の声部連結を鮮明に切り取ることができます。従来の理論ではやはり分析においてもV-Iの動きに注目することが最重要視され、3度で進行する箇所は単なる同機能の延長といって切り捨てられることもしばしば。そこにスポットライトを当てることになるネオ・リーマン理論は、従来の理論を補完する補佐的なツールとして考えたときに、すごく有用なものに思えます。
例えば転調に関してはドミナント系コードやディミニッシュセブンスの推進力を利用したものが代表的ですが、先ほどのベートーヴェンの“第九”に見たようなFmからD♭への進行で完結するヌルッとした転調は基本的なレパートリーの中にありません。それゆえ従来理論による分析のみだけだと、あの例は「ベートーヴェンはやっぱり革新的ですね」みたいな“例外”的パターンとして流されてしまう可能性もありそうです。
しかしネオ・リーマン理論があれば、こうした用例をPLRの名の下に分類・収集することができ、用例をもとに再現性のある技術として実践に還元できます。
またコード間の接続だけに注目するため、キー(ひいてはコードのディグリー)を特定する必要がないという点で、調性が崩壊していく19世紀ロマン派の音楽分析に便利そうだというのはこのたった2つの例を見ても感じるところです。
分析において調を確定させること、根音の変化に着目すること、5度進行を基本とすること。これらは従来理論での基本的な教義ですが、ネオ・リーマン理論は結果としてこれら全てにアンチの立場を取ることになります。分析に調は要らない、根音変化より共通音の連結に着目し、3度進行を基本とする──。正反対であるからこそ、これまで見落としてきたものを発見するオルタナティブ・ツールとしての期待と関心が寄せられているわけです。
さて、「PLR操作」と「トネッツ」というネオ・リーマン理論の最もキャッチーな部分は紹介できましたが、「ヘキサトニックサイクル・シリンダー」のようなちょっと応用的なアイテムがまだ少し残っています。しかしながらここまでの内容だけでもかなり目新しい部分が多かったはずなので、ここで一旦記事を区切ろうと思います。
Continue